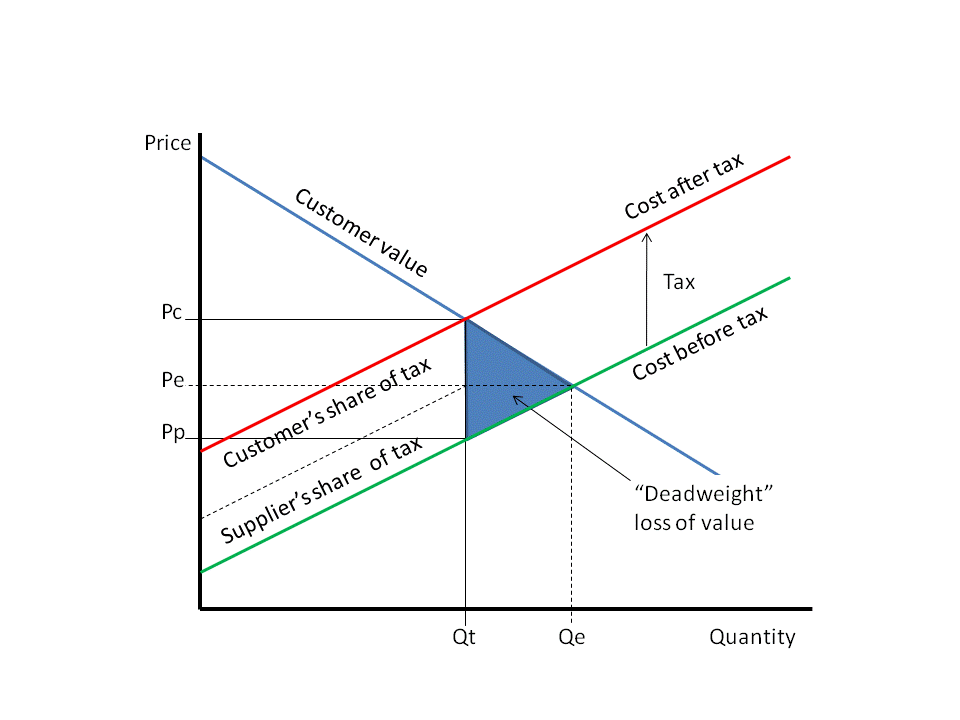
I’ve mentioned this before: most taxes cause economic losses. These are costs, both expended for physical things as well as opportunity costs, that result from people changing their behavior in response to a tax. The two components of this happens are:
Deadweight losses (reduced economic activity)
Tax compliance/avoidance
The first component is a result of the tax resulting in higher costs, and therefore higher prices, which reduces how much economic activity happens. Since all economic activity results in a net gain to the participants in the associated trade, a loss of those trades is an opportunity cost loss. For example, if a sales tax is increased, stores would have to raise prices and people would buy fewer things (and perhaps make more things at home). Or if income tax is increased, people may decide to work less than they would have before (eg working fewer hours, spending more time between jobs, choosing a lower-wage but more satisfying job, or retiring earlier). People may also demand higher wages, which increases unemployment. The chart below shows this component of deadweight loss:
Green/red lines are supply curves, blue line is the demand curve, blue triangle is the deadweight loss.
The other component is (legal and illegal) tax avoidance - people will pay a good accountant to minimize their tax burden. People will also take risks to avoid taxes (like not reporting cash transactions). For a tax payer, its in their personal interest to spend up to a dollar for every dollar in saved taxes. If it costs $99 for a person to save $100 in taxes, most people would probably do it, but as a result 99% of the taxes raised would be wastefully burned. The cost of tax compliance in the US has been estimated at about $550 billion/year for federal taxes alone. This is over 10% of the taxes collected.
Here I’m going to estimate the economic losses of income taxes over a range of tax rates using a simple model. But know that this kind of calculation applies similarly to business taxes, sales taxes, and the non-land fraction of property taxes.
For the supply and demand curves for labor, elasticity of supply and demand have had a number of estimates over the years (see note 1). Elasticity of demand in the US has been estimated from between -0.23 to around -0.6. Elasticity of supply in the US has been estimated at between 0.68 and 1.38. For the following charts, I’ll use an elasticity of demand of -0.4 and an elasticity of supply of 0.7, because those were close to most of the estimates I saw.
Translating this into a chart (see math in note 2) would look something like the following (note that the zeros of the equation are not calibrated, just made up, but we only care about the slopes for this analysis so it doesn’t matter):

The brown triangular area is the deadweight loss (see note 3 for the math). The red supply curve has a different slope than the green supply curve because of how an income tax rate means that more taxes will be paid by someone who has a higher income (a flat tax would make both slopes the same).
This is a chart of the total surplus (consumer + producer), total tax collected, and deadweight loss:

You can see the purple line representing the total tax collected has a peak at a tax rate of around 60%. This may be familiar to you as the Laffer curve. This 60% estimate is roughly in line with numerous empirical estimates done for various countries (which generally place the tax revenue maximizing point at 50-75%). Increasing tax rates beyond this peak benefits neither the society nor the government, as lower taxes would be collected despite the higher tax rate.
And here is a chart showing the deadweight loss as a fraction of the tax collected for a range of tax percents from 0-100% (see note 2):
As you can see, the deadweight loss increases exponentially as the tax rate increases, until at about 75% the fraction passes 100% of the tax collected (the point circled in yellow). So based on this estimate, one should expect a 20% tax rate to have almost triple the deadweight loss that a 10% tax rate has.
However, because deadweight loss has an exponential relationship with tax rate, every additional percent added to the tax rate has more deadweight loss than the last. What we should really care about is what fraction of the additional revenue raised by an additional percent of tax is lost as deadweight loss. This chart shows that:
This indicates that tax rates higher than about 43% have no realistic possibility of being good for the economy, since the marginal deadweight loss is higher than the tax revenue raised (see note 11).
Doing some math to estimate the deadweight loss for people at different income ranges in the US, the estimate comes to a deadweight loss of 12% of the taxes raised in 2020 (see note 10).
In addition to the deadweight loss, there are economic losses as a result of tax compliance, which its estimated costs the US economy $546 billion/year, 11% of the taxes raised.
Combining these two costs, we should expect current a total economic loss due to federal tax collection (not including any state or local income taxes) to be about 23% of the tax collected. That isn’t negligible, and means that government spending would need to be 30% more efficient than market spending in order to make the loss worthwhile.
States that collect income tax push the deadweight loss up quite a bit. For example, California collects an income tax of around 8%, which would push the deadweight loss up by about 60% to 17.6% (a total economic loss of 28.6%) while only collecting 32% more revenue (than the federal tax). It has been estimated that income taxes collected comes with an economic loss of 30% of the taxes collected, which matches up very well with my estimated total loss of 28.6%.
The highest tax rates in the country approach 52% (37% federal + 10.9% in New York state + 3.876% in NYC), and these very clearly exceed the amount that has any realistic possibly of being good for the country/state collectively.
This is of course a very rough estimate because there is no one linear elasticity for labor demand or supply, and there is no one price of labor in the market. This should nonetheless be indicative of the effect that higher taxation has. And note that this does not take into account business taxes (including the part of payroll taxes that businesses pay), which would further push up the marginal deadweight loss. Maybe I’ll add that in as a short update post at some point.
In any case, the conclusion to take away from this is that marginal deadweight loss increases quickly and the highest income tax rates in the US (when combining federal, state, and local) likely destroy more wealth than they bring in as government revenue. It has become trendy to want to increase income taxes on the rich, but there are practical limits to this where we are shooting ourselves in the foot by doing so. If people in the US really want to tax the rich more, increasing income taxes for the highest tax brackets are no longer a good way to do it. Increasing property taxes would likely be a far better way to do that, but of course land value taxes would be far better than that.
Notes:
Elasticities of demand (ie employers’ demand for workers) have been estimated at around -0.4 in Germany, -0.23 and between -0.49 and -0.93 in the US and elasticities of supply (ie people’s willingness to supply their own labor by taking a job) have been estimated at 0.71-0.75 in australia, 0.6, 0.68, and 1.38 in the US. Estimation Of Labor Demand Elasticity For The RMSM-LP by Hong-Ghi Min found that the minimum demand elasticity estimate was -0.12 and maximum was -1.54.
SE = Supply Elasticity
DE = Demand Elasticity
price supplied (before tax) = SE*quantity
price supplied (after tax) = (SE*quantity) / (1-tax rate)
price demanded = 5 + DE*quantity (note the 5 is completely arbitrary)
price (before tax) = SE*quantity = 5 + DE*quantity →
(SE-DE)*quantity = 5 →
quantity (before tax) = 5/(SE-DE) →
price (before tax) = SE*5/(SE-DE)
price (after tax) = (SE*quantity) / (1-tax rate) = 5 + DE*quantity →
SE*quantity = (5 + DE*quantity) * (1-tax rate) →
SE*quantity = 5 + DE*quantity - 5 * tax rate - DE * quantity * tax rate →
SE*quantity - DE*quantity + DE * quantity * tax rate = 5 - 5 * tax rate →
quantity*((SE-DE) + DE * tax rate) = 5 - 5 * tax rate →
quantity (after tax) = 5*(1 - tax rate)/((SE-DE) + DE * tax rate)
price (after tax) = 5 * (1 + (1 - tax rate)/((SE/DE-1) + tax rate)
total tax collected = price * quantity * tax rate
reduced price = price (before tax) - price (after tax))
reduced quantity = quantity (before tax) - quantity (after tax)
supply price (at reduced quantity before tax) = SE*quantity (after tax)deadweight loss = reduced quantity * (price (after tax) - supply price (at reduced quantity before tax))/2 =
1/2
* (5/(SE-DE) - 5*(1 - tax rate)/((SE-DE) + DE * tax rate))
* (5 * (1 + (1 - tax rate)/((SE/DE-1) + tax rate) - SE*5/(SE-DE) - 5*(1 - tax rate)/((SE-DE))
reduced quantity * (price (after tax) - price (at reduced quantity before tax))/2
= 1/2 * (4.484 - (1 - tax rate) / (0.224 - 0.08 * tax rate))
* (5 - (1 - tax rate) / (0.56 - 0.2 * tax rate)- 0.72 * (1 - tax rate) / (0.224 - 0.08 * tax rate)
)
→ using an equation solver →initial surplus = initial demand price * quantity (before tax) / 2
= 5 * 5/(SE-DE) / 2 = 12.5 / (SE-DE)
surplus = initial surplus - deadweight lossdeadweight loss (as a fraction of the tax collected) =
(1/2 * (4.484 - (1 - tax rate) / (0.224 - 0.08 * tax rate)) * (5 - (1 - tax rate) / (0.56 - 0.2 * tax rate) - 0.72 * (1 - tax rate) / (0.224 - 0.08 *tax rate) ))/((5 - (1 - x)/(0.56 - 0.2 * tax rate)) * (1 - tax rate)/(0.224 - 0.08 * tax rate) * tax rate)
→ using an equation solver →Average income tax rates for different income levels:
* percentile range:
Top X Atr = (Top Y Atr * Y + Top X-Y atr * (X-Y)) / X →
Top X-Y atr = (Top X Atr * X - Top Y Atr * Y)/(X-Y)
where:
* Atr = Average tax rate
* X is the larger percentile
* Y is the smalle percentile
* Top X-Y atr is a percentile range. For example if X is 5% and Y is 1%, it
represents the 2nd percentile to 5th percentile range.
* Top 1%: 26%
* 2nd-5th percentile: (.26*1 + x*4) / 5 = .224 → x = (.224*5 - .26)/4 = 21.5%
* 10th-6th percentile: (.224*5 + x*5) / 10 = .203 → x = .406 - .224 = 18.2%
* 25th-11th percentile: (.203*10 + x*15) / 25 = .171 → x = (.171 * 25 - 2.03)/15 = 14.97%
* 50th-26th percentile: (.171*25 + x*25) / 50 = .148 → x = (.148 * 2 - .171) = 12.5%
* 100th-51st percentile: 3.1%Share of federal income taxes paid for different income levels:
* Top 1%: 42.3%
* 2nd-5th percentile: .627 - .423 = 20.4%
* 10th-6th percentile: .737 - .627 = 11%
* 25th-11th percentile: .885 - .737 = 14.8%
* 50th-26th percentile: .977 - .885 = 9.2%
* 100th-51st percentile: 2.3%Average income tax rates including payroll taxes for different income levels:
* Top 1%: 26% + 0.6% + 3.8% = 30.4%
* 2nd-5th percentile: .215+.062×168600/(136000/.224) + .038 = 21.5% + 2.7% + 3.8% = 28%
* 10th-6th percentile: .182+.062×168600/((220000+152000)/2) = 18.2% + 5.6% + 2.9% = 26.7%
* 25th-11th percentile: 14.97% + 6.2% + 2.9% = 24.07%
* 50th-26th percentile: 12.5% + 6.2% + 2.9% = 21.6%
* 100th-51st percentile: 3.1% + 6.2% + 2.9% = 12.2%Share of federal income and payroll taxes paid for different income levels:
* Total additional taxes contributed by payroll taxes: 42.3*0.044/0.26 + 20.4*.065/0.215 + 11*.085/0.182 + 14.8*.081/0.1497 + 9.2*.081/0.125 + 2.3*.081/0.023 = 40.5% (note that this is lower than .349/.485 because almost half of payroll taxes are paid by the employer).
* Top 1%: (42.3 + 42.3*0.044/0.26))/140.5 = 35.2%
* 2nd-5th percentile: (20.4 + 20.4*.065/0.215)/140.5 = 18.9%
* 10th-6th percentile: (11 + 11*.085/0.182)/140.5 = 11.5%
* 25th-11th percentile: (14.8 + 14.8*.081/0.1497)/140.5 = 16.2%
* 50th-26th percentile: (9.2 + 9.2*.081/0.125)/140.5 = 10.8%
* 100th-51st percentile: (2.3 + 2.3*.081/0.023)/140.5 = 7.4%Estimate of deadweight loss in the US (2020) based on average tax rates (including payroll taxes) for different income levels:
* Top 1%: 14.2%
* 2nd-5th percentile: 12.8%
* 10th-6th percentile: 12.1%
* 25th-11th percentile: 11.9%
* 50th-26th percentile: 9.1%
* 100th-51st percentile: 4.6%Estimate of total deadweight loss in the US (2020) based on the above and the share of total income taxes paid by each group:
.142*.352 + .128*.189 + .121*.115 + .119*.162 + .091*.108 + .046*.074 = 12%For the tax collected to be put to worthwhile use above a tax rate of 43% (in this example), the government would have to use it in a way that is more than twice as efficient as what the market would have done with the money. This is usually not realistic, tho there may be certain situations where it’s possible. Perhaps something like national defense is something with high value the market itself can’t provide efficiently. But it seems very unlikely that a 43% tax rate would be necessary to fund national defense. Thus, I’d say its unrealistic that a rate higher than that is ever a good thing.